The Idea

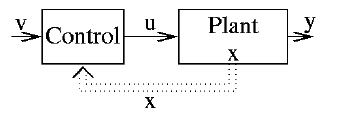
Observations of the human body reveal an interplay between the passive evolution of a physical system (the human body) and the influences of an active, complex controller (the nervous system). Given the available tools for modeling physical systems, it is convenient to model these two elements separately, as illustrated in Figure 2.

**Figure:** A block diagram of human motion. The **Plant** models the physical evolution of the system, but there is also significant structure in the peripheral nervous system, here lumped into **Control**
$\begin{figure}\centerline{\psfig{figure=figs/human.eps,width=80mm}} \end{figure}$

In the classical Observer model, the Observer has direct access to the control being applied to the Plant, as shown in Figure 3.

**Figure:** This is the classic Observer configuration, where the control input is available to to the Observer.
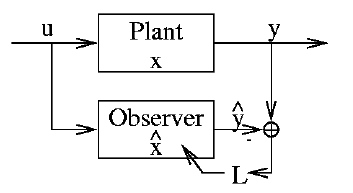$\begin{figure}\centerline{\psfig{figure=figs/classic.eps,width=80mm}} \end{figure}$

In the case of human motion, direct access to control signals is very difficult, or impossible. So the situation we're presented with is better modeled by Figure 4. In this formulation, in the place of the control signal, is an estimated control signal. The estimated control signal is a function of the observation error, and possibly the Observer state.

**Figure:** The proposed Observer configuration for the case when the control signal is unavailable.
$\begin{figure}\centerline{\psfig{figure=figs/nocontrol.eps,width=80mm}} \end{figure}$

In Figure 4, $\tilde{y}$ is the observation error. When the above Observer is implemented as a Kalman filter, the observation errors are the Innovations. For an optimally tuned filter, the Innovations are a zero mean Gaussian noise process if the state disturbance is a zero mean Gaussian noise process. When the control signal isn't zero mean Gaussian, this is expressed as a bias in the Innovations. Thus the Innovations process is a natural place to look for structure in the controller.

The structure of the controller provides important constraints on the system evolution. Understanding those constraints is an important element of understanding motion that we're observing. However, it is very difficult to explicitly model the human nervous system, so the approach of using observed data to estimate probability distributions over this control space is very appealing.