Mathematics

Eigenvalues

An eigenvalue and eigenvector of a square matrix A are a scalar 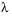and a nonzero vector v that satisfy

This section explains:

• Eigenvalue decomposition
• Problems associated with defective (not diagonalizable) matrices
• The use of Schur decomposition to avoid problems associated with eigenvalue decomposition

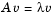
Eigenvalue Decomposition

With the eigenvalues on the diagonal of a diagonal matrix 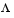and the corresponding eigenvectors forming the columns of a matrix V, we have

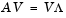
If V is nonsingular, this becomes the eigenvalue decomposition

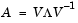
A good example is provided by the coefficient matrix of the ordinary differential equation in the previous section.

• A =
       0    -6    -1
       6     2   -16
      -5    20   -10
  

The statement

• lambda = eig(A)
  

produces a column vector containing the eigenvalues. For this matrix, the eigenvalues are complex.

• lambda =
       -3.0710         
       -2.4645+17.6008i
       -2.4645-17.6008i
  

The real part of each of the eigenvalues is negative, so 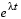approaches zero as t increases. The nonzero imaginary part of two of the eigenvalues, 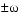, contributes the oscillatory component, 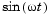, to the solution of the differential equation.

With two output arguments, eig computes the eigenvectors and stores the eigenvalues in a diagonal matrix.

• [V,D] = eig(A)
  
  V =
    -0.8326         0.2003 - 0.1394i   0.2003 + 0.1394i
    -0.3553        -0.2110 - 0.6447i  -0.2110 + 0.6447i
    -0.4248        -0.6930            -0.6930          
  
  D =
    -3.0710                 0                 0         
          0           -2.4645+17.6008i        0         
          0                 0           -2.4645-17.6008i
  

The first eigenvector is real and the other two vectors are complex conjugates of each other. All three vectors are normalized to have Euclidean length, norm(v,2), equal to one.

The matrix V*D*inv(V), which can be written more succinctly as V*D/V, is within roundoff error of A. And, inv(V)*A*V, or V\A*V, is within roundoff error of D.

Defective Matrices

Some matrices do not have an eigenvector decomposition. These matrices are defective, or not diagonalizable. For example,

• A = [ 6    12    19
       -9   -20   -33
        4     9    15 ]
  

For this matrix

• [V,D] = eig(A)
  

produces

• V =
  
     -0.4741   -0.4082   -0.4082
      0.8127    0.8165    0.8165
     -0.3386   -0.4082   -0.4082
  
  D =
  
     -1.0000         0         0
           0    1.0000         0
           0         0    1.0000
  

There is a double eigenvalue at 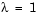. The second and third columns of V are the same. For this matrix, a full set of linearly independent eigenvectors does not exist.

The optional Symbolic Math Toolbox extends the capabilities of MATLAB by connecting to Maple, a powerful computer algebra system. One of the functions provided by the toolbox computes the Jordan Canonical Form. This is appropriate for matrices like our example, which is 3-by-3 and has exactly known, integer elements.

• [X,J] = jordan(A)
  
  X =
     -1.7500    1.5000    2.7500
      3.0000   -3.0000   -3.0000
     -1.2500    1.5000    1.2500
  
  J =
      -1     0     0
       0     1     1
       0     0     1
  

The Jordan Canonical Form is an important theoretical concept, but it is not a reliable computational tool for larger matrices, or for matrices whose elements are subject to roundoff errors and other uncertainties.

Schur Decomposition in MATLAB Matrix Computations

The MATLAB advanced matrix computations do not require eigenvalue decompositions. They are based, instead, on the Schur decomposition

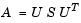
where U is an orthogonal matrix and S is a block upper triangular matrix with 1-by-1 and 2-by-2 blocks on the diagonal. The eigenvalues are revealed by the diagonal elements and blocks of S, while the columns of U provide a basis with much better numerical properties than a set of eigenvectors. The Schur decomposition of our defective example is

• [U,S] = schur(A)
  
  U =
     -0.4741    0.6648    0.5774
      0.8127    0.0782    0.5774
     -0.3386   -0.7430    0.5774
  
  S =
     -1.0000   20.7846   -44.6948
           0    1.0000    -0.6096
           0         0     1.0000
  

The double eigenvalue is contained in the lower 2-by-2 block of S.

Note    If A is complex, schur returns the complex Schur form, which is upper triangular with the eigenvalues of A on the diagonal.

Matrix Powers and Exponentials

Singular Value Decomposition