Mathematics

Singular Value Decomposition

A singular value and corresponding singular vectors of a rectangular matrix A are a scalar 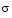and a pair of vectors u and v that satisfy

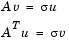
With the singular values on the diagonal of a diagonal matrix 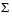and the corresponding singular vectors forming the columns of two orthogonal matrices U and V, we have

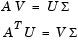
Since U and V are orthogonal, this becomes the singular value decomposition

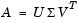
The full singular value decomposition of an m-by-n matrix involves an m-by-m U, an m-by-n 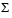, and an n-by-n V. In other words, U and V are both square and 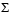is the same size as A. If A has many more rows than columns, the resulting U can be quite large, but most of its columns are multiplied by zeros in 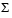. In this situation, the economy sized decomposition saves both time and storage by producing an m-by-n U, an n-by-n 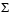and the same V.

The eigenvalue decomposition is the appropriate tool for analyzing a matrix when it represents a mapping from a vector space into itself, as it does for an ordinary differential equation. On the other hand, the singular value decomposition is the appropriate tool for analyzing a mapping from one vector space into another vector space, possibly with a different dimension. Most systems of simultaneous linear equations fall into this second category.

If A is square, symmetric, and positive definite, then its eigenvalue and singular value decompositions are the same. But, as A departs from symmetry and positive definiteness, the difference between the two decompositions increases. In particular, the singular value decomposition of a real matrix is always real, but the eigenvalue decomposition of a real, nonsymmetric matrix might be complex.

For the example matrix

• A =
       9     4
       6     8
       2     7
  

the full singular value decomposition is

• [U,S,V] = svd(A)
  U =
      -0.6105    0.7174    0.3355
      -0.6646   -0.2336   -0.7098
      -0.4308   -0.6563    0.6194
  S =
     14.9359         0
           0    5.1883
           0         0
  V =
      -0.6925    0.7214
      -0.7214   -0.6925
  

You can verify that U*S*V' is equal to A to within roundoff error. For this small problem, the economy size decomposition is only slightly smaller.

• [U,S,V] = svd(A,0)
  U =
      -0.6105    0.7174
      -0.6646   -0.2336
      -0.4308   -0.6563
  S =
     14.9359         0
           0    5.1883
  V =
      -0.6925    0.7214
      -0.7214   -0.6925
  

Again, U*S*V' is equal to A to within roundoff error.

Eigenvalues

Polynomials and Interpolation