

| Mathematics |   |
Examples: Applying the ODE Initial Value Problem Solvers
This section contains several examples that illustrate the kinds of problems you can solve:
rigidode)
vdpode)
fem1ode)
brussode)
ballode)
orbitode)
hb1dae)
Example: Simple Nonstiff Problem
rigidode illustrates the solution of a standard test problem proposed by Krogh for solvers intended for nonstiff problems [8].
The ODEs are the Euler equations of a rigid body without external forces.
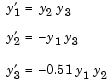
For your convenience, the entire problem is defined and solved in a single M-file. The differential equations are coded as a subfunction f. Because the example calls the ode45 solver without output arguments, the solver uses the default output function odeplot to plot the solution components.
To run this example, click on the example name, or type rigidode at the command line.
function rigidode %RIGIDODE Euler equations of a rigid body without external forces tspan = [0 12]; y0 = [0; 1; 1]; % Solve the problem using ode45 ode45(@f,tspan,y0); % ------------------------------------------------------------ function dydt = f(t,y) dydt = [ y(2)*y(3) -y(1)*y(3) -0.51*y(1)*y(2) ];
Example: Stiff Problem (van der Pol Equation)
vdpode illustrates the solution of the van der Pol problem described in Example: The van der Pol Equation, µ = 1000 (Stiff). The differential equations
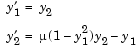
involve a constant parameter 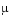 .
.
As 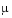 increases, the problem becomes more stiff, and the period of oscillation becomes larger. When
increases, the problem becomes more stiff, and the period of oscillation becomes larger. When 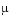 is
is 1000 the equation is in relaxation oscillation and the problem is very stiff. The limit cycle has portions where the solution components change slowly and the problem is quite stiff, alternating with regions of very sharp change where it is not stiff (quasi-discontinuities).
By default, the solvers in the ODE suite that are intended for stiff problems approximate Jacobian matrices numerically. However, this example provides a subfunction J(t,y,mu) to evaluate the Jacobian matrix 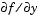 analytically at
analytically at (t,y) for 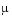 =
= mu. The use of an analytic Jacobian can improve the reliability and efficiency of integration.
To run this example, click on the example name, or type vdpode at the command line. From the command line, you can specify a value of 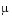 as an argument to
as an argument to vdpode. The default is 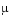 = 1000.
= 1000.
function vdpode(MU) %VDPODE Parameterizable van der Pol equation (stiff for large MU) if nargin < 1 MU = 1000; % default end tspan = [0; max(20,3*MU)]; % Several periods y0 = [2; 0]; options = odeset('Jacobian',@J); [t,y] = ode15s(@f,tspan,y0,options,MU); plot(t,y(:,1)); title(['Solution of van der Pol Equation, \mu = ' num2str(MU)]); xlabel('time t'); ylabel('solution y_1'); axis([tspan(1) tspan(end) -2.5 2.5]); --------------------------------------------------------------- function dydt = f(t,y,mu) dydt = [ y(2) mu*(1-y(1)^2)*y(2)-y(1) ]; --------------------------------------------------------------- function dfdy = J(t,y,mu) dfdy = [ 0 1 -2*mu*y(1)*y(2)-1 mu*(1-y(1)^2) ];
Example: Finite Element Discretization
fem1ode illustrates the solution of ODEs that result from a finite element discretization of a partial differential equation. The value of N in the call fem1ode(N) controls the discretization, and the resulting system consists of N equations. By default, N is 19.
This example involves a mass matrix. The system of ODEs comes from a method of lines solution of the partial differential equation
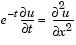
with initial condition 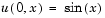 and boundary conditions
and boundary conditions 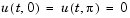 . An integer
. An integer 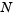 is chosen,
is chosen, 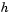 is defined as
is defined as 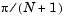 , and the solution of the partial differential equation is approximated at
, and the solution of the partial differential equation is approximated at 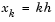 for k = 0, 1, ..., N+1 by
for k = 0, 1, ..., N+1 by
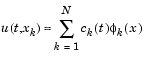
Here 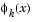 is a piecewise linear function that is 1 at
is a piecewise linear function that is 1 at 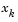 and 0 at all the other
and 0 at all the other 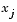 . A Galerkin discretization leads to the system of ODEs
. A Galerkin discretization leads to the system of ODEs

and the tridiagonal matrices 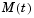 and
and 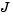 are given by
are given by
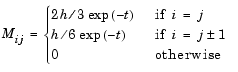
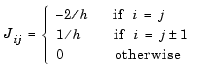
The initial values 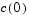 are taken from the initial condition for the partial differential equation. The problem is solved on the time interval
are taken from the initial condition for the partial differential equation. The problem is solved on the time interval 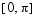 .
.
indicate that the problem is of the form 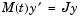 . The subfunction
. The subfunction mass(t,N) evaluates the time-dependent mass matrix 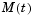 and
and J is the constant Jacobian.
To run this example, click on the example name, or type fem1ode at the command line. From the command line, you can specify a value of 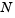 as an argument to
as an argument to fem1ode. The default is 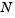 = 19.
= 19.
function fem1ode(N) %FEM1ODE Stiff problem with a time-dependent mass matrix if nargin < 1 N = 19; end h = pi/(N+1); y0 = sin(h*(1:N)'); tspan = [0; pi]; % The Jacobian is constant. e = repmat(1/h,N,1); % e=[(1/h) ... (1/h)]; d = repmat(-2/h,N,1); % d=[(-2/h) ... (-2/h)]; J = spdiags([e d e], -1:1, N, N); options = odeset('Mass',@mass,'MStateDependence','none', ... 'Jacobian',J); [t,y] = ode15s(@f,tspan,y0,options,N); surf((1:N)/(N+1),t,y); set(gca,'ZLim',[0 1]); view(142.5,30); title(['Finite element problem with time-dependent mass ' ... 'matrix, solved by ODE15S']); xlabel('space ( x/\pi )'); ylabel('time'); zlabel('solution'); %-------------------------------------------------------------- - function out = f(t,y,N) h = pi/(N+1); e = repmat(1/h,N,1); % e=[(1/h) ... (1/h)]; d = repmat(-2/h,N,1); % d=[(-2/h) ... (-2/h)]; J = spdiags([e d e], -1:1, N, N); out = J*y; %-------------------------------------------------------------- - function M = mass(t,N) h = pi/(N+1); e = repmat(exp(-t)*h/6,N,1); % e(i)=exp(-t)*h/6 e4 = repmat(4*exp(-t)*h/6,N,1); M = spdiags([e e4 e], -1:1, N, N);
Example: Large, Stiff Sparse Problem
brussode illustrates the solution of a (potentially) large stiff sparse problem. The problem is the classic "Brusselator" system [3] that models diffusion in a chemical reaction
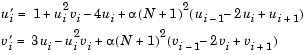
and is solved on the time interval [0,10] with 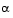 = 1/50 and
= 1/50 and
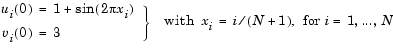
There are 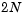 equations in the system, but the Jacobian is banded with a constant width 5 if the equations are ordered as
equations in the system, but the Jacobian is banded with a constant width 5 if the equations are ordered as 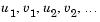
In the call brussode(N), where N corresponds to 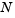 , the parameter
, the parameter N 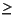
2 specifies the number of grid points. The resulting system consists of 2N equations. By default, N is 20. The problem becomes increasingly stiff and the Jacobian increasingly sparse as N increases.
The subfunction f(t,y,N) returns the derivatives vector for the Brusselator problem. The subfunction jpattern(N) returns a sparse matrix of 1s and 0s showing the locations of nonzeros in the Jacobian 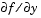 . The example assigns this matrix to the property
. The example assigns this matrix to the property JPattern, and the solver uses the sparsity pattern to generate the Jacobian numerically as a sparse matrix. Providing a sparsity pattern can significantly reduce the number of function evaluations required to generate the Jacobian and can accelerate integration. For the Brusselator problem, if the sparsity pattern is not supplied, 2N evaluations of the function are needed to compute the 2N-by-2N Jacobian matrix. If the sparsity pattern is supplied, only four evaluations are needed, regardless of the value of N.
To run this example, click on the example name, or type brussode at the command line. From the command line, you can specify a value of 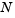 as an argument to
as an argument to brussode. The default is 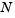 = 20.
= 20.
function brussode(N) %BRUSSODE Stiff problem modeling a chemical reaction if nargin<1 N = 20; end tspan = [0; 10]; y0 = [1+sin((2*pi/(N+1))*(1:N)); repmat(3,1,N)]; options = odeset('Vectorized','on','JPattern',jpattern(N)); [t,y] = ode15s(@f,tspan,y0,options,N); u = y(:,1:2:end); x = (1:N)/(N+1); surf(x,t,u); view(-40,30); xlabel('space'); ylabel('time'); zlabel('solution u'); title(['The Brusselator for N = ' num2str(N)]); % -------------------------------------------------------------- function dydt = f(t,y,N) c = 0.02 * (N+1)^2; dydt = zeros(2*N,size(y,2)); % preallocate dy/dt % Evaluate the two components of the function at one edge of % the grid (with edge conditions). i = 1; dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ... c*(1-2*y(i,:)+y(i+2,:)); dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ... c*(3-2*y(i+1,:)+y(i+3,:)); % Evaluate the two components of the function at all interior % grid points. i = 3:2:2*N-3; dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ... c*(y(i-2,:)-2*y(i,:)+y(i+2,:)); dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ... c*(y(i-1,:)-2*y(i+1,:)+y(i+3,:)); % Evaluate the two components of the function at the other edge % of the grid (with edge conditions). i = 2*N-1; dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ... c*(y(i-2,:)-2*y(i,:)+1); dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ... c*(y(i-1,:)-2*y(i+1,:)+3); % -------------------------------------------------------------- function S = jpattern(N) B = ones(2*N,5); B(2:2:2*N,2) = zeros(N,1); B(1:2:2*N-1,4) = zeros(N,1); S = spdiags(B,-2:2,2*N,2*N);
Example: Simple Event Location
ballode models the motion of a bouncing ball. This example illustrates the event location capabilities of the ODE solvers.
The equations for the bouncing ball are
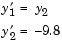
In this example, the event function is coded in a subfunction events
isterminal = 1 or 0, respectively) when value = 0
-1 |
Detect zero crossings in the negative direction only |
0 |
Detect all zero crossings |
1 |
Detect zero crossings in the positive direction only |
The length of value, isterminal, and direction is the same as the number of event functions. The ith element of each vector, corresponds to the ith event function. For an example of more advanced event location, see orbitode (Example: Advanced Event Location).
In ballode, setting the Events property to @events causes the solver to stop the integration (isterminal = 1) when the ball hits the ground (the height y(1) is 0) during its fall (direction = -1). The example then restarts the integration with initial conditions corresponding to a ball that bounced.
To run this example, click on the example name, or type ballode at the command line.
function ballode %BALLODE Run a demo of a bouncing ball. tstart = 0; tfinal = 30; y0 = [0; 20]; refine = 4; options = odeset('Events',@events,'OutputFcn', @odeplot,... 'OutputSel',1,'Refine',refine); set(gca,'xlim',[0 30],'ylim',[0 25]); box on hold on; tout = tstart; yout = y0.'; teout = []; yeout = []; ieout = []; for i = 1:10 % Solve until the first terminal event. [t,y,te,ye,ie] = ode23(@f,[tstart tfinal],y0,options); if ~ishold hold on end % Accumulate output. nt = length(t); tout = [tout; t(2:nt)]; yout = [yout; y(2:nt,:)]; teout = [teout; te]; % Events at tstart are never reported. yeout = [yeout; ye]; ieout = [ieout; ie]; ud = get(gcf,'UserData'); if ud.stop break; end % Set the new initial conditions, with .9 attenuation. y0(1) = 0; y0(2) = -.9*y(nt,2); % A good guess of a valid first time step is the length of % the last valid time step, so use it for faster computation. options = odeset(options,'InitialStep',t(nt)-t(nt-refine),... 'MaxStep',t(nt)-t(1)); tstart = t(nt); end plot(teout,yeout(:,1),'ro') xlabel('time'); ylabel('height'); title('Ball trajectory and the events'); hold off odeplot([],[],'done'); % -------------------------------------------------------------- function dydt = f(t,y) dydt = [y(2); -9.8]; % -------------------------------------------------------------- function [value,isterminal,direction] = events(t,y) % Locate the time when height passes through zero in a % decreasing direction and stop integration. value = y(1); % Detect height = 0 isterminal = 1; % Stop the integration direction = -1; % Negative direction only
Example: Advanced Event Location
orbitode illustrates the solution of a standard test problem for those solvers that are intended for nonstiff problems. It traces the path of a spaceship traveling around the moon and returning to the earth. (Shampine and Gordon [8], p.246).
The orbitode problem is a system of the four equations shown below
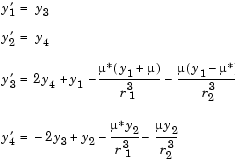
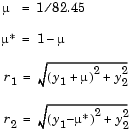
The first two solution components are coordinates of the body of infinitesimal mass, so plotting one against the other gives the orbit of the body. The initial conditions have been chosen to make the orbit periodic. The value of 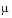 corresponds to a spaceship traveling around the moon and the earth. Moderately stringent tolerances are necessary to reproduce the qualitative behavior of the orbit. Suitable values are
corresponds to a spaceship traveling around the moon and the earth. Moderately stringent tolerances are necessary to reproduce the qualitative behavior of the orbit. Suitable values are 1e-5 for RelTol and 1e-4 for AbsTol.
The events subfunction includes event functions which locate the point of maximum distance from the starting point and the time the spaceship returns to the starting point. Note that the events are located accurately, even though the step sizes used by the integrator are not determined by the location of the events. In this example, the ability to specify the direction of the zero crossing is critical. Both the point of return to the initial point and the point of maximum distance have the same event function value, and the direction of the crossing is used to distinguish them.
To run this example, click on the example name, or type orbitode at the command line. The example uses the output function odephase2 to produce the two-dimensional phase plane plot and let you to see the progress of the integration.
function orbitode %ORBITODE Restricted three-body problem tspan = [0 7]; y0 = [1.2; 0; 0; -1.04935750983031990726]; options = odeset('RelTol',1e-5,'AbsTol',1e-4,... 'OutputFcn',@odephas2,'Events',@events); [t,y,te,ye,ie] = ode45(@f,tspan,y0,options); plot(y(:,1),y(:,2),ye(:,1),ye(:,2),'o'); title ('Restricted three body problem') ylabel ('y(t)') xlabel ('x(t)') % -------------------------------------------------------------- function dydt = f(t,y) mu = 1 / 82.45; mustar = 1 - mu; r13 = ((y(1) + mu)^2 + y(2)^2) ^ 1.5; r23 = ((y(1) - mustar)^2 + y(2)^2) ^ 1.5; dydt = [ y(3) y(4) 2*y(4) + y(1) - mustar*((y(1)+mu)/r13) - ... mu*((y(1)-mustar)/r23) -2*y(3) + y(2) - mustar*(y(2)/r13) - mu*(y(2)/r23) ]; % -------------------------------------------------------------- function [value,isterminal,direction] = events(t,y) % Locate the time when the object returns closest to the % initial point y0 and starts to move away, and stop integration. % Also locate the time when the object is farthest from the % initial point y0 and starts to move closer. % % The current distance of the body is % % DSQ = (y(1)-y0(1))^2 + (y(2)-y0(2))^2 % = <y(1:2)-y0,y(1:2)-y0> % % A local minimum of DSQ occurs when d/dt DSQ crosses zero % heading in the positive direction. We can compute d(DSQ)/dt as % % d(DSQ)/dt = 2*(y(1:2)-y0)'*dy(1:2)/dt = 2*(y(1:2)-y0)'*y(3:4) % y0 = [1.2; 0]; dDSQdt = 2 * ((y(1:2)-y0)' * y(3:4)); value = [dDSQdt; dDSQdt]; isterminal = [1; 0]; % Stop at local minimum direction = [1; -1]; % [local minimum, local maximum]
Example: Differential-Algebraic Problem
hb1dae reformulates the hb1ode example as a differential-algebraic equation (DAE) problem. The Robertson problem coded in hb1ode is a classic test problem for codes that solve stiff ODEs.
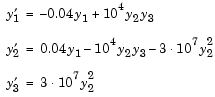
| Note The Robertson problem appears as an example in the prolog to LSODI [4]. |
In hb1ode, the problem is solved with initial conditions 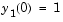 ,
, 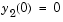 ,
, 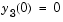 to steady state. These differential equations satisfy a linear conservation law that is used to reformulate the problem as the DAE
to steady state. These differential equations satisfy a linear conservation law that is used to reformulate the problem as the DAE
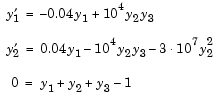
Obviously these equations do not have a solution for 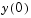 with components that do not sum to 1. The problem has the form of
with components that do not sum to 1. The problem has the form of 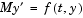 with
with
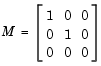
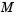 is obviously singular, but
is obviously singular, but hb1dae does not inform the solver of this. The solver must recognize that the problem is a DAE, not an ODE. Similarly, although consistent initial conditions are obvious, the example uses an inconsistent value 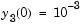 to illustrate computation of consistent initial conditions.
to illustrate computation of consistent initial conditions.
To run this example, click on the example name, or type hb1dae at the command line. Note that hb1dae:
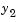 than on the other components. This is because
than on the other components. This is because 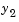 is much smaller than the other components and its major change takes place in a relatively short time.
is much smaller than the other components and its major change takes place in a relatively short time.
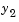 .
.
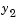 by 104 to make
by 104 to make 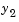 visible when plotting it with the rest of the solution.
visible when plotting it with the rest of the solution.
function hb1dae %HB1DAE Stiff differential-algebraic equation (DAE) % A constant, singular mass matrix M = [1 0 0 0 1 0 0 0 0]; % Use an inconsistent initial condition to test initialization. y0 = [1; 0; 1e-3]; tspan = [0 4*logspace(-6,6)]; % Use the LSODI example tolerances. The 'MassSingular' property % is left at its default 'maybe' to test the automatic detection % of a DAE. options = odeset('Mass',M,'RelTol',1e-4,... 'AbsTol',[1e-6 1e-10 1e-6],'Vectorized','on'); [t,y] = ode15s(@f,tspan,y0,options); y(:,2) = 1e4*y(:,2); semilogx(t,y); ylabel('1e4 * y(:,2)'); title(['Robertson DAE problem with a Conservation Law, '... 'solved by ODE15S']); xlabel('This is equivalent to the stiff ODEs coded in HB1ODE.'); % -------------------------------------------------------------- function out = f(t,y) out = [ -0.04*y(1,:) + 1e4*y(2,:).*y(3,:) 0.04*y(1,:) - 1e4*y(2,:).*y(3,:) - 3e7*y(2,:).^2 y(1,:) + y(2,:) + y(3,:) - 1 ];
 | Changing ODE Integration Properties | Questions and Answers, and Troubleshooting |  |