

| Mathematics |   |
Changing ODE Integration Properties
The default integration properties in the ODE solvers are selected to handle common problems. In some cases, you can improve ODE solver performance by overriding these defaults. You do this by supplying the solvers with one or more property values in an options structure.
In this and subsequent property tables, the most commonly used properties are listed first, followed by more advanced properties.
| Properties Category |
Property Name |
| Error control |
RelTol, AbsTol, NormControl |
| Solver output |
OutputFcn, OutputSel, Refine, Stats |
| Jacobian matrix |
Jacobian, JPattern, Vectorized |
| Step-size |
InitialStep, MaxStep |
| Mass matrix and DAEs |
Mass, MStateDependence, MvPattern, MassSingular, InitialSlope |
| Event location |
Events |
ode15s-specific |
MaxOrder, BDF |
Creating and Maintaining an ODE Options Structure
Creating an Options Structure. The odeset function creates an options structure that you can pass as an argument to any of the ODE solvers. To create an options structure, odeset accepts property name/property value pairs using the syntax
In the resulting structure, options, the named properties have the specified values. Any unspecified properties contain default values in the solvers. For all properties, it is sufficient to type only the leading characters that uniquely identify the property name. odeset ignores case for property names.
With no input arguments, odeset displays all property names and their possible values. It indicates defaults with {}.
Modifying an Existing Options Structure. To modify an existing options structure, oldopts, use
This sets options equal to the existing structure oldopts, overwrites any values in oldopts that are respecified using name/value pairs, and adds any new pairs to the structure. The modified structure is returned as an output argument. In the same way, the command
combines the structures oldopts and newopts. In the output argument, any values in the second argument overwrite those in the first argument.
Querying Options. The odeget function extracts property values from an options structure created with odeset.
This functions returns the value of the specified property, or an empty matrix [], if the property value is unspecified in the options structure.
As with odeset, it is sufficient to type only the leading characters that uniquely identify the property name. Case is ignored for property names.
Error Control Properties
At each step, the solver estimates the local error e in the ith component of the solution. This error must be less than or equal to the acceptable error, which is a function of the specified relative tolerance, RelTol, and the specified absolute tolerance, AbsTol.
For routine problems, the ODE solvers deliver accuracy roughly equivalent to the accuracy you request. They deliver less accuracy for problems integrated over "long" intervals and problems that are moderately unstable. Difficult problems may require tighter tolerances than the default values. For relative accuracy, adjust RelTol. For the absolute error tolerance, the scaling of the solution components is important: if |y| is somewhat smaller than AbsTol, the solver is not constrained to obtain any correct digits in y. You might have to solve a problem more than once to discover the scale of solution components.
Roughly speaking, this means that you want RelTol correct digits in all solution components except those smaller than thresholds AbsTol(i). Even if you are not interested in a component y(i) when it is small, you may have to specify AbsTol(i) small enough to get some correct digits in y(i) so that you can accurately compute more interesting components
The following table describes the error control properties. Use odeset to set the properties.
The solver output properties let you control the output that the solvers generate. Use odeset to set these properties.
| Property |
Value |
Description | ||
OutputFcn |
Function {odeplot} |
Installable output function. The solver calls this function after every successful integration step. For example, sets the OutputFcn property to an output function, myfun, that can be passed to an ODE solver.The output function must be of the form The solver calls the specified output function with the following flags. Note that the syntax of the call differs with the flag. The function must respond appropriately: | ||
|
init |
The solver calls myfun(tspan,y0,'init') before beginning the integration to allow the output function to initialize. tspan and y0 are the input arguments to the ODE solver. |
||
|
{none} |
The solver calls status = myfun(t,y) after each integration step on which output is requested. t contains points where output was generated during the step, and y is the numerical solution at the points in t. If t is a vector, the ith column of y corresponds to the ith element of t.When length(tspan) > 2 the output is produced at every point in tspan. When length(tspan) = 2 the output is produced according to the Refine option.myfun must return a status output value of 0 or 1. If status = 1, the solver halts integration. You can use this mechanism, for instance, to implement a Stop button. |
||
|
done |
The solver calls myfun([],[],'done') when integration is complete to allow the output function to perform any cleanup chores. |
||
|
You can use these general purpose output functions or you can edit them to create your own. Type help function at the command line for more information. | |||
OutputSel |
Vector of indices |
Vector of indices specifying which components of the solution vector are to be passed to the output function. For example, if you want to use the odeplot output function, but you want to plot only the first and third components of the solution, you can do this usingBy default, the solver passes all components of the solution to the output function. | ||
Refine |
Positive integer |
Increases the number of output points by a factor of Refine. If Refine is 1, the solver returns solutions only at the end of each time step. If Refine is n >1, the solver subdivides each time step into n smaller intervals, and returns solutions at each time point. Refine does not apply when length(tspan)>2.
Refine are computed by means of continuous extension formulas. These are specialized formulas used by the ODE solvers to obtain accurate solutions between computed time steps without significant increase in computation time. | ||
Stats |
on | {off} |
Specifies whether the solver should display statistics about its computations. By default, Stats is off. If it is on, after solving the problem the solver displays: | ||
Jacobian Matrix Properties
The stiff ODE solvers often execute faster if you provide additional information about the Jacobian matrix 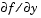 , a matrix of partial derivatives of the function that defines the differential equations.
, a matrix of partial derivatives of the function that defines the differential equations.
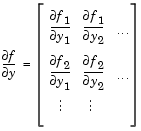
The Jacobian matrix properties pertain only to those solvers for stiff problems (ode15s, ode23s, ode23t, and ode23tb) for which the Jacobian matrix 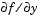 can be critical to reliability and efficiency. If you do not provide a function to calculate the Jacobian, these solvers approximate the Jacobian numerically using finite differences. In this case, you may want to use the
can be critical to reliability and efficiency. If you do not provide a function to calculate the Jacobian, these solvers approximate the Jacobian numerically using finite differences. In this case, you may want to use the Vectorized, or JPattern properties.
The following table describes the Jacobian matrix properties. Use odeset to set these properties.
| Property |
Value |
Description |
Jacobian |
Function | constant matrix |
A constant matrix or a function that evaluates the Jacobian. Supplying an analytical Jacobian often increases the speed and reliability of the solution for stiff problems. Set this property to a function FJac, where FJac(t,y) computes 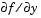 , or to the constant value of , or to the constant value of 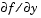 . .The Jacobian for the stiff van der Pol problem shown above can be coded as |
JPattern |
Sparse matrix of {0,1} |
Sparsity pattern with 1s where there might be nonzero entries in the Jacobian. It is used to generate a sparse Jacobian matrix numerically. Set this property to a sparse matrix 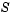 with with 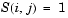 if component if component 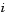 of of 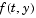 depends on component depends on component 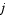 of of 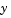 , and 0 otherwise. The solver uses this sparsity pattern to generate a sparse Jacobian matrix numerically. If the Jacobian matrix is large and sparse, this can greatly accelerate execution. For an example using the , and 0 otherwise. The solver uses this sparsity pattern to generate a sparse Jacobian matrix numerically. If the Jacobian matrix is large and sparse, this can greatly accelerate execution. For an example using the JPattern property, see Example: Large, Stiff Sparse Problem (brussode). |
Vectorized |
on | {off} |
Set on to inform the solver that you have coded the ODE function F so that F(t,[y1 y2 ...]) returns [F(t,y1) F(t,y2) ...]. This allows the solver to reduce the number of function evaluations required to compute all the columns of the Jacobian matrix, and may significantly reduce solution time.With the MATLAB array notation, it is typically an easy matter to vectorize an ODE function. For example, the stiff van der Pol example shown previously can be vectorized by introducing colon notation into the subscripts and by using the array power ( .^) and array multiplication (.*) operators. |
Step-Size Properties
The step-size properties let you specify the size of the first step the solver tries, potentially helping it to better recognize the scale of the problem. In addition, you can specify bounds on the sizes of subsequent time steps.
The following table describes the step-size properties. Use odeset to set these properties.
| Property |
Value |
Description |
InitialStep |
Positive scalar |
Suggested initial step size. InitialStep sets an upper bound on the magnitude of the first step size the solver tries. If you do not set InitialStep, the initial step size is based on the slope of the solution at the initial time tspan(1), and if the slope of all solution components is zero, the procedure might try a step size that is much too large. If you know this is happening or you want to be sure that the solver resolves important behavior at the start of the integration, help the code start by providing a suitable InitialStep. |
MaxStep |
Positive scalar {0.1*abs(t0-tf)} |
Upper bound on solver step size. If the differential equation has periodic coefficients or solutions, it may be a good idea to set MaxStep to some fraction (such as 1/4) of the period. This guarantees that the solver does not enlarge the time step too much and step over a period of interest. Do not reduce MaxStep:
|
|
Mass Matrix and DAE Properties
The solvers of the ODE suite can solve ODEs of the form
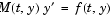
|
(14-2) |
with a mass matrix 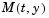 that can be sparse.
that can be sparse.
When 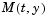 is nonsingular, the equation above is equivalent to
is nonsingular, the equation above is equivalent to 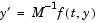 and the ODE has a solution for any initial values
and the ODE has a solution for any initial values 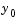 at
at 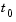 . The more general form (Equation 14-2) is convenient when you express a model naturally in terms of a mass matrix. For large, sparse
. The more general form (Equation 14-2) is convenient when you express a model naturally in terms of a mass matrix. For large, sparse 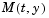 , solving Equation 14-2 directly reduces the storage and runtime needed to solve the problem.
, solving Equation 14-2 directly reduces the storage and runtime needed to solve the problem.
When 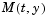 is singular, then
is singular, then 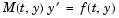 is a differential-algebraic equation (DAE). A DAE has a solution only when
is a differential-algebraic equation (DAE). A DAE has a solution only when 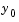 is consistent, that is, there exists an initial slope
is consistent, that is, there exists an initial slope 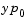 such that
such that
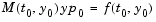 . If
. If 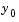 and
and 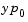 are not consistent, the solver treats them as guesses, attempts to compute consistent values that are close to the guesses, and continues to solve the problem. For DAEs of index 1, solving an initial value problem with consistent initial conditions is much like solving an ODE.
are not consistent, the solver treats them as guesses, attempts to compute consistent values that are close to the guesses, and continues to solve the problem. For DAEs of index 1, solving an initial value problem with consistent initial conditions is much like solving an ODE.
The ode15s and ode23t solvers can solve DAEs of index 1. For examples of DAE problems, see hb1dae (Example: Differential-Algebraic Problem) and amp1dae.
The following table describes the mass matrix and DAE properties. Use odeset to set these properties.
| Property |
Value |
Description |
Mass |
Constant matrix | function |
Constant mass matrix or a function that evaluates the mass matrix 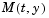 . For problems . For problems 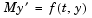 set this property to the value of the constant mass matrix set this property to the value of the constant mass matrix 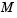 . For problems . For problems 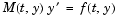 , set this property to a function , set this property to a function Mfun, where Mfun(t,y) evaluates the mass matrix 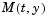 . When solving DAEs, it is advantageous to formulate the problem so that . When solving DAEs, it is advantageous to formulate the problem so that 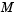 is a diagonal matrix (a semi-explicit DAE). The is a diagonal matrix (a semi-explicit DAE). The ode23s solver can only solve problems with a constant mass matrix 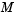 . . For example problems, see fem1ode (Example: Finite Element Discretization), fem2ode, or batonode. |
MStateDependence |
none | {weak} | strong |
Dependence of the mass matrix on 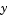 . Set this property to . Set this property to none for problems 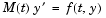 . Both . Both weak and strong indicate 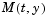 , but , but weak results in implicit solvers using approximations when solving algebraic equations. |
MvPattern |
Sparse matrix |
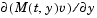 sparsity pattern. Set this property to a sparse matrix sparsity pattern. Set this property to a sparse matrix 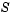 with with 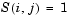 if for any if for any 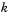 , the , the 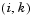 component of component of 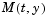 depends on component depends on component 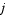 of of 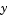 , and 0 otherwise. For use with the , and 0 otherwise. For use with the ode15s, ode23t, and ode23tb solvers when MStateDependence is strong. See burgersode as an example. |
MassSingular |
yes | no | {maybe} |
Indicates whether the mass matrix is singular. Set this property to no if the mass matrix is not singular and you are using either the ode15s or ode23t solver. The default value of maybe causes the solver to test whether the problem is a DAE, i.e., whether 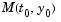 is singular. is singular. For an example of a problem with a mass matrix, see Example: Finite Element Discretization ( fem1ode). |
InitialSlope |
Vector | {zero vector} |
Vector representing the consistent initial slope 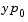 , where , where 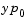 satisfies satisfies 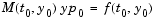 . The default is the zero vector. . The default is the zero vector. This property is for use with the ode15s and ode23t solvers when solving DAEs. |
Event Location Property
In some ODE problems the times of specific events are important, such as the time at which a ball hits the ground, or the time at which a spaceship returns to the earth. While solving a problem, the ODE solvers can detect such events by locating transitions to, from, or through zeros of user-defined functions.
The following table describes the Events property. Use odeset to set this property.
| String |
Value |
Description |
Events |
Function |
Function that includes one or more event functions. The function is of the formvalue, isterminal, and direction are vectors for which the ith element corresponds to the ith event function:
the solver returns these outputs as TE, YE, and IE respectively. If you call the solver as the solver returns these outputs as For examples that use an event function, see Example: Simple Event Location ( |
ode15s Properties
ode15s is a variable-order solver for stiff problems. It is based on the numerical differentiation formulas (NDFs). The NDFs are generally more efficient than the closely related family of backward differentiation formulas (BDFs), also known as Gear's methods. The ode15s properties let you choose between these formulas, as well as specifying the maximum order for the formula used.
The following table describes the ode15s properties. Use odeset to set these properties.
| Property |
Value |
Description |
MaxOrder |
1 | 2 | 3 | 4 | {5} |
The maximum order formula used to compute the solution. |
BDF |
on | {off} |
Specifies whether you want to use the BDFs instead of the default NDFs. Set BDF on to have ode15s use the BDFs.For both the NDFs and BDFs, the formulas of orders 1 and 2 are A-stable (the stability region includes the entire left half complex plane). The higher order formulas are not as stable, and the higher the order the worse the stability. There is a class of stiff problems (stiff oscillatory) that is solved more efficiently if MaxOrder is reduced (for example to 2) so that only the most stable formulas are used. |
 | Solving ODE Problems | Examples: Applying the ODE Initial Value Problem Solvers |  |