

| Mathematics |   |
MATLAB Partial Differential Equation Solver
pdepe
The PDE Solver
The MATLAB PDE solver, pdepe, solves initial-boundary value problems for systems of parabolic and elliptic PDEs in the one space variable 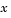 and time
and time 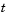 . There must be at least one parabolic equation in the system.
. There must be at least one parabolic equation in the system.
The pdepe solver converts the PDEs to ODEs using a second-order accurate spatial discretization based on a set of nodes specified by the user. The discretization method is described in [9]. The time integration is done with ode15s. The pdepe solver exploits the capabilities of ode15s for solving the differential-algebraic equations that arise when Equation 14-4 contains elliptic equations, and for handling Jacobians with a specified sparsity pattern. ode15s changes both the time step and the formula dynamically.
After discretization, elliptic equations give rise to algebraic equations. If the elements of the initial conditions vector that correspond to elliptic equations are not "consistent" with the discretization, pdepe tries to adjust them before beginning the time integration. For this reason, the solution returned for the initial time may have a discretization error comparable to that at any other time. If the mesh is sufficiently fine, pdepe can find consistent initial conditions close to the given ones. If pdepe displays a message that it has difficulty finding consistent initial conditions, try refining the mesh. No adjustment is necessary for elements of the initial conditions vector that correspond to parabolic equations.
PDE Solver Basic Syntax
The basic syntax of the solver is
| Note Correspondences given are to terms used in Introduction to PDE Problems. |
m |
Specifies the symmetry of the problem. |
pdefun |
Function that defines the components of the PDE. It computes the terms 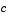 , , 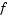 , and , and 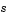 in Equation 14-4, and has the form in Equation 14-4, and has the formwhere x and t are scalars, and u and dudx are vectors that approximate the solution 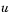 and its partial derivative with respect to and its partial derivative with respect to 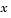 . . c, f, and s are column vectors. c stores the diagonal elements of the matrix 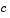 . . |
icfun |
Function that evaluates the initial conditions. It has the form When called with an argument x, icfun evaluates and returns the initial values of the solution components at x in the column vector u. |
bcfun |
Function that evaluates the terms 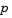 and and 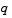 of the boundary conditions. It has the form of the boundary conditions. It has the form where |
xmesh |
Vector [x0, x1, ..., xn] specifying the points at which a numerical solution is requested for every value in tspan. x0 and xn correspond to 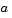 and and 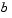 , respectively. , respectively. Second-order approximation to the solution is made on the mesh specified in xmesh must satisfy x0 < x1 < ... < xn. The length of xmesh must be 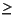 3. |
tspan |
Vector [
The elements of |
The output argument sol is a three-dimensional array, such that:
sol(:,:,k) approximates component k of the solution 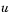 .
.
sol(i,:,k) approximates component k of the solution at time tspan(i) and mesh points xmesh(:).
sol(i,j,k) approximates component k of the solution at time tspan(i) and the mesh point xmesh(j).
Additional PDE Solver Arguments
For more advanced applications, you can also specify as input arguments solver options and additional parameters that are passed to the PDE functions.
|
Structure of optional parameters that change the default integration properties. This is the seventh input argument. See Changing PDE Integration Properties for more information. |
p1,p2... |
Parameters that the solver passes to pdefun, icfun, and bcfun. The solver passes any input parameters that follow the options argument to pdefun, icfun, and bcfun every time it calls them. Use options = [] as a placeholder if you set no options. In the pdefun argument list, parameters follow x, t, u, and dudx. In the icfun argument list, parameters follow x.In the bcfun argument list, parameters follow xl, ul, xr, ur, and t.See the |
 | Introduction to PDE Problems | Solving PDE Problems |  |