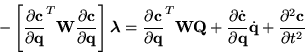Hard Constraints

Hard constraints represent absolute limitations imposed on the system. One example of a kinematic constraint is a skeletal joint. Lagrangian dynamics can be used to satisfy such hard constraints by choosing a state vector the describes only the degrees of freedom left to the system[7]. This requires that the constraints be solved analytically at model-building time.

While this formulation is very efficient, it requires an analytical solution of the constraints to exist. It also precludes modification of the constraint structure at run-time. Our model instead follows the virtual work formulation [21]. In a virtual work formulation, all the links in a model have full range of unconstrained motion. Hard kinematic constraints on the system are be represented as a special set of forces ${\bf C}$:

$$\ddot{{\bf q}} = {\bf W} \cdot ( {\bf Q} + {\bf C} )$$ (1)

These constraints are functions of the systems state, and may also be time varying:

$${\bf C} = {\bf c}({\bf q}, t)$$

The constraints are defined so that they are satisfied when ${\bf c}({\bf q}, t) = 0$. If the constraint is satisfied at time t₀, then it will remain satisfied for all time if $\dot{\bf c} = 0$ and $\ddot{\bf c} = 0$ also remain zero for all time t>t₀. Since ${\bf c}$ depends on q and t, differentiation gives us:

$$\dot{\bf c} = \frac{\partial {\bf c}}{\partial {\bf q}} \dot{\bf q} + \frac{\partial {\bf c}}{\partial t}$$

and another differentiation:

$$\ddot{\bf c} = \frac{\partial {\bf c}}{\partial {\bf q}} ... ...bf q}} \dot{\bf q} + \frac{\partial^2 {\bf c}}{\partial t^2}$$ (2)

Setting $\ddot{\bf c} = 0$ and combining Equation 2 with Equation 1 gives us a system of linear equations that describes the set of ${\bf C}$ that are consistent with continued constraint satisfaction:

$$\frac{\partial {\bf c}}{\partial {\bf q}} W ({\bf Q}+{\bf C... ...ot{\bf q} + \frac{\partial^{2} {\bf c}}{\partial t^{2}} = 0$$ (3)

This system, in general, has many solutions. One method of chosing a solution is the concept of virtual work. Stated simply, virtual work requires that constraints never change the energy of the system; constraints must do no work. This can be accomplished by insuring that ${\bf C}\partial{\bf q} = 0$. Since $\partial{\bf q}$ is required to be in the null space of the constraint Jacobian:

$$\frac{\partial \dot{{\bf c}}}{\partial {\bf q}} d{\bf q} = 0$$

Requiring the constraint forces to lie in the null space complement satisfies the virtual work requirement:

$$C = {\mbox{\boldmath$ \lambda $}} \frac{\partial \dot{{\bf c}}}{\partial {\bf q}}$$ (4)

Combining Equation 4 with Equation 3 results in an equation with only the vector of unknowns , ${\mbox{\boldmath$\ \lambda $}}$:

$$-\left[ \frac{\partial {\bf c}}{\partial {\bf q}}^{T} {... ...} \dot{\bf q} + \frac{\partial^{2} {\bf c}}{\partial t^{2}}$$

This equation can be rewritten to emphasize its linear nature. ${\bf J}$ is the constraint Jacobian, ${\mbox{\boldmath$\ \kappa $}}$ is the vector on the right-hand side, and ${\mbox{\boldmath$\ \lambda $}}$ is the vector of unknown Lagrange multipliers:

$$- {\bf J}^{T} {\bf W} {\bf J} {\mbox{\boldmath$ \lambda $}} = {\mbox{\boldmath$ \kappa $}}$$ (5)