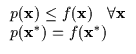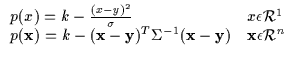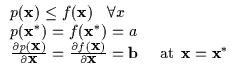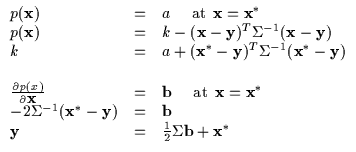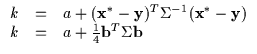The bound must make contact with the function (Equation 6.4) at the current operating point for the maximization process to behave as described earlier.
The bound's tangent plane should be parallel to the function's tangent plane at the current operating point as in Equation 6.5. Otherwise, there will be an intersection between the function and the lower bound and the lower bound will rise above it, violating the lower bound assumption.
Finally, the bound should be as 'close' to the function as possible to approximate the function properly. Typically, a lower bound which falls away from the function too quickly is not very likely to cause rapid optimization. In other words, what is desired is that the maximum of the bound is close to the maximum of the function. Let us focus on the quadratic bound described earlier (Equation 6.6).
We use ![]() to denote the location parameter which moves the
locus of the parabola's maximum around. The k parameter varies the
maximum's amplitude. Finally, note the
to denote the location parameter which moves the
locus of the parabola's maximum around. The k parameter varies the
maximum's amplitude. Finally, note the ![]() (or
(or ![]() in 1
dimension). This is the scale (or shape) parameter which changes the
shape and orientation of the parabola. We can also define the inverse
of the scale parameter as
in 1
dimension). This is the scale (or shape) parameter which changes the
shape and orientation of the parabola. We can also define the inverse
of the scale parameter as
![]() (or
(or
![]() ).
).
Typically, the scalar parameter k and the location parameter ![]() are determined directly from the constraints in
Equation 6.4 and
Equation 6.5. However, the scale parameter remains
to be determined. Evidently, it must be chosen so that the lower bound
property of the quadratic is not violated. However, we also would like
to maximize the determinant of the scale parameter as given by
Equation 6.7.
are determined directly from the constraints in
Equation 6.4 and
Equation 6.5. However, the scale parameter remains
to be determined. Evidently, it must be chosen so that the lower bound
property of the quadratic is not violated. However, we also would like
to maximize the determinant of the scale parameter as given by
Equation 6.7.
This statement is not as obvious as the previous two requirements and we justifiy it subsequently.
Suppose that Requirements 1 and 2 have been resolved and,
specifically, we have the computed Equation 6.8
to obain real values (a and ![]() ). These expressions can be
manipulated further for the case of the quadratic as in
Equation 6.9 yielding two constraint expressions
(containing the constant terms a and
). These expressions can be
manipulated further for the case of the quadratic as in
Equation 6.9 yielding two constraint expressions
(containing the constant terms a and ![]() ).
).
The expressions in Equation 6.9 can then be used
to isolate k and express it exclusively in terms of the constants
![]() ,
a and
,
a and ![]() as well as the still free shape
parameter
as well as the still free shape
parameter ![]() .
Note the isolated k in
Equation 6.10 and its relationship to
.
Note the isolated k in
Equation 6.10 and its relationship to ![]() (or
W equivalently). As we increase
(or
W equivalently). As we increase ![]() (or decrease |W|), we are
effectively increasing k. The larger
(or decrease |W|), we are
effectively increasing k. The larger ![]() yields high values
of k. Since maximizing the quadratic bound will move our current
locus from
yields high values
of k. Since maximizing the quadratic bound will move our current
locus from ![]() to
to ![]() the higher the
the higher the
![]() the higher the value of the function we can
jump to. It is obvious that the widest parabola or maximal
the higher the value of the function we can
jump to. It is obvious that the widest parabola or maximal ![]() is desirable since it is more likely to allow higher jumps in the
function being optimized. In reality, we would ideally like to
maximize the expression
is desirable since it is more likely to allow higher jumps in the
function being optimized. In reality, we would ideally like to
maximize the expression
![]() over all the
elements of the
over all the
elements of the ![]() .
Thus the requirement for maximal
.
Thus the requirement for maximal ![]() or maximal k can be interchanged.
or maximal k can be interchanged.
In fact, we typically begin by finding the optimal ![]() 6.2 and then
isolating the corresponding k and
6.2 and then
isolating the corresponding k and ![]() .
These three quantities
are really functions of the operating point
.
These three quantities
are really functions of the operating point ![]() (once the
function to optimize, f(), is specified of course) and can be
expressed as functions of each other as well. This concept is
demonstrated in concrete examples that will follow.
(once the
function to optimize, f(), is specified of course) and can be
expressed as functions of each other as well. This concept is
demonstrated in concrete examples that will follow.