| (6) |
It only remains to bring information from the human model back down to the initial stages of the vision system. In the absence of this information, the pixel classification decisions were forced to rely solely on temporal smoothness constraints in the 2-D image plane. The decision rule takes the form:
Since the human model exists in 3-D a projection operation is required
to convert the model's 3-D predictions into the 2-D features of the
vision system. Given the current state of the model ![]() ,
it is
possible to compute the state of an individual link that matches a specific
tracked feature (say the hand), and compute 3-D means and covariances.
Then, given a model of the camera, it is possible to calculate the
projection of that state into 2-D and call it
,
it is
possible to compute the state of an individual link that matches a specific
tracked feature (say the hand), and compute 3-D means and covariances.
Then, given a model of the camera, it is possible to calculate the
projection of that state into 2-D and call it
![]() .
For the first moment (the mean) that calculation is a
perspective projection:
.
For the first moment (the mean) that calculation is a
perspective projection:
![\begin{displaymath}
{\mbox{\boldmath$ \mu $}}^{*} = \left[ \begin{array}{c} u \\...
...frac{z}{f}} \\
\frac{y}{1 + \frac{z}{f}} \end{array} \right]
\end{displaymath}](img49.gif)
Since the vision system uses a stochastic framework, it is necessary to
represent this link projection as a probabilistic model:
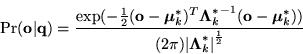
Now that the 3-D model features are projected into the 2-D camera coordinates, they can be integrated into the 2-D probabilistic decision framework. This provides the Maximum A Posteriori decision rule with the much better prior information contained in the higher-level models.