The low-level features extracted from video comprise the final element of
our system. Our system tracks regions that are visually similar, and
spatially coherent: blobs [17,12]. The blob spatial
statistics are described in terms of their second-order properties for
which we denote
![]() as the mean and
as the mean and
![]() as the
covariance. For computational convenience we will interpret this as a
Gaussian model, so the probability of an observaion
as the
covariance. For computational convenience we will interpret this as a
Gaussian model, so the probability of an observaion ![]() (of a certain
color and position within the image), given a blob model is:
(of a certain
color and position within the image), given a blob model is:
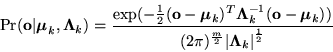
Like other representations used in computer vision and signal analysis, including superquadrics, modal analysis, and eigen representations, blobs represent the global aspects of the shape and can be augmented with higher-order statistics to attain more detail if the data supports it. The reduction of degrees of freedom from individual pixels to blob parameters is a form of regularization which allows the ill-conditioned problem to be solved in a principled and stable way.
These 2-D features are the input to the 3-D blob estimation formulation used by Azarbayejani and Pentland [2]. This relates the 2-D distribution of pixel values to a tracked object's 3-D position and orientation. In our current system we track the hands and head using their color and shape characteristics; the observation equation therefore relates the distribution of hand/face pixel values to the probability distribution of the 3-D state variables that characterize the skeletal models' hand and head links.
These observations supply constraints on the underlying 3-D human model.
Due to their probabilistic nature, observations are easily modeled as soft
constraints. Observations are integrated into the dynamic evolution of the
system by modeling them as descriptions of potential fields, as discussed
in Section 2.1.2. The simplest such model is a linear spring
model with a fixed a priori weighting ![]() :
: