

| Mathematics |   |
Eigenvalues and Singular Values
Two functions are available which compute a few specified eigenvalues or singular values. svds is based on eigs which uses ARPACK [6].
| Function |
Description |
|
Few eigenvalues |
|
Few singular values |
These functions are most frequently used with sparse matrices, but they can be used with full matrices or even with linear operators defined by M-files.
finds the k eigenvalues and corresponding eigenvectors of the matrix A which are nearest the "shift" sigma. If sigma is omitted, the eigenvalues largest in magnitude are found. If sigma is zero, the eigenvalues smallest in magnitude are found. A second matrix, B, may be included for the generalized eigenvalue problem
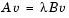
finds the k largest singular values of A and
finds the k smallest singular values.
set up the five-point Laplacian difference operator on a 65-by-65 grid in an L-shaped, two-dimensional domain. The statements
show that A is a matrix of order 2945 with 14,473 nonzero elements.
computes the smallest eigenvalue and eigenvector. Finally,
distributes the components of the eigenvector over the appropriate grid points and produces a contour plot of the result.
The numerical techniques used in eigs and svds are described in [6].
 | Simultaneous Linear Equations | Selected Bibliography |  |