

| Mathematics |   |
Initial Value ODE Problem Solvers
These are the initial value problem solvers. The table lists the kind of problem you can solve with each solver, and the method each solver uses.
| Solver |
Solves These Kinds of Problems |
Method |
|
Nonstiff differential equations |
Runge-Kutta |
|
Nonstiff differential equations |
Runge-Kutta |
|
Nonstiff differential equations |
Adams |
|
Stiff differential equations and DAEs |
NDFs (BDFs) |
|
Stiff differential equations |
Rosenbrock |
|
Moderately stiff differential equations and DAEs |
Trapezoidal rule |
|
Stiff differential equations |
TR-BDF2 |
ODE Solution Evaluation
If you call an ODE solver with one output argument, it returns a structure that you can use to evaluate the solution at any point on the interval of integration.
| Function |
Description |
|
Evaluate the numerical solution using output of ODE solvers. |
ODE Solver Properties Handling
An options structure contains named integration properties whose values are passed to the solver, and which affect problem solution. Use these functions to create, alter, or access an options structure.
| Function |
Description |
|
Create or alter options structure for input to ODE solvers. |
|
Extract properties from options structure created with odeset. |
ODE Solver Output Functions
If an output function is specified, the solver calls the specified function after every successful integration step. You can use odeset to specify one of these sample functions as the OutputFcn property, or you can modify them to create your own functions.
| Function |
Description |
|
Time-series plot |
|
Two-dimensional phase plane plot |
|
Three-dimensional phase plane plot |
|
Print to command window |
ODE Initial Value Problem Examples
These examples illustrate the kinds of problems you can solve in MATLAB. Click the example name to see the code in an editor. Type the example name at the command line to run it.
Note
The Differential Equations Examples browser enables you to view the code for the ODE examples and DAE examples. You can also run the examples from the browser. Click on these links to invoke the browser, or type odeexamples('ode')or odeexamples('dae')at the command line.
|
| Example |
Description |
amp1dae |
Stiff DAE - electrical circuit |
ballode |
Simple event location - bouncing ball |
batonode |
ODE with time- and state-dependent mass matrix - motion of a baton |
brussode |
Stiff large problem - diffusion in a chemical reaction (the Brusselator) |
burgersode |
ODE with strongly state-dependent mass matrix - Burger's equation solved using a moving mesh technique |
fem1ode |
Stiff problem with a time-dependent mass matrix - finite element method |
fem2ode |
Stiff problem with a constant mass matrix - finite element method |
hb1dae |
Stiff DAE from a conservation law |
hb1ode |
Stiff problem solved on a very long interval - Robertson chemical reaction |
orbitode |
Advanced event location - restricted three body problem |
rigidode |
Nonstiff problem - Euler equations of a rigid body without external forces |
vdpode |
Parameterizable van der Pol equation (stiff for large 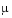 ) ) |
 | Initial Value Problems for ODEs and DAEs | Introduction to Initial Value ODE Problems |  |