Differential Equations (Mathematics)

Mathematics

Boundary Value Problem Solver

This section describes:

The BVP solver, bvp4c
BVP solver basic syntax
Additional BVP solver arguments

The BVP Solver

The function bvp4c solves two-point boundary value problems for ordinary differential equations (ODEs). It integrates a system of first-order ordinary differential equations

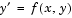
on the interval 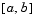, subject to general two-point boundary conditions

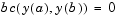
It can also accommodate unknown parameters for problems of the form

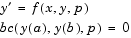
In this case, the number of boundary conditions must be sufficient to determine the solution and the unknown parameters. For more information, see Finding Unknown Parameters.

bvp4c produces a solution that is continuous on 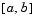and has a continuous first derivative there. You can use the function deval and the output of bvp4c to evaluate the solution at specific points on the interval of integration.

bvp4c is a finite difference code that implements the 3-stage Lobatto IIIa formula. This is a collocation formula and the collocation polynomial provides a C¹-continuous solution that is fourth-order accurate uniformly in the interval of integration. Mesh selection and error control are based on the residual of the continuous solution.

The collocation technique uses a mesh of points to divide the interval of integration into subintervals. The solver determines a numerical solution by solving a global system of algebraic equations resulting from the boundary conditions, and the collocation conditions imposed on all the subintervals. The solver then estimates the error of the numerical solution on each subinterval. If the solution does not satisfy the tolerance criteria, the solver adapts the mesh and repeats the process. The user must provide the points of the initial mesh as well as an initial approximation of the solution at the mesh points.

BVP Solver Basic Syntax

The basic syntax of the BVP solver is

```
sol = bvp4c(odefun,bcfun,solinit)
```

The input arguments are:

odefun
Function that evaluates the differential equations. It has the basic form
dydx = odefun(x,y)
where x is a scalar, and dydx and y are column vectors. odefun can also accept a vector of unknown parameters and a variable number of known parameters.

bcfun
Function that evaluates the residual in the boundary conditions. It has the basic form
res = bcfun(ya,yb)
where ya and yb are column vectors representing y(a) and y(b), and res is a column vector of the residual in satisfying the boundary conditions. bcfun can also accept a vector of unknown parameters and a variable number of known parameters.

solinit
Structure with fields x and y:

x
Ordered nodes of the initial mesh. Boundary conditions are imposed at a = solinit.x(1) and b = solinit.x(end).

y
Initial guess for the solution with solinit.y(:,i) a guess for the solution at the node solinit.x(i).

The structure can have any name, but the fields must be named x and y. It can also contain a vector that provides an initial guess for unknown parameters. You can form solinit with the helper function bvpinit. See the bvpinit reference page for details.

`odefun`	Function that evaluates the differential equations. It has the basic form `dydx = odefun(x,y)` where `x` is a scalar, and `dydx` and `y` are column vectors. `odefun` can also accept a vector of unknown parameters and a variable number of known parameters.
`bcfun`	Function that evaluates the residual in the boundary conditions. It has the basic form `res = bcfun(ya,yb)` where `ya` and `yb` are column vectors representing `y(a)` and `y(b)`, and `res` is a column vector of the residual in satisfying the boundary conditions. `bcfun` can also accept a vector of unknown parameters and a variable number of known parameters.
`solinit`	Structure with fields `x` and `y`:
	`x`	Ordered nodes of the initial mesh. Boundary conditions are imposed at a = `solinit.x(1)` and b = `solinit.x(end)`.
	`y`	Initial guess for the solution with `solinit.y(:,i)` a guess for the solution at the node `solinit.x(i)`.
	The structure can have any name, but the fields must be named `x` and `y`. It can also contain a vector that provides an initial guess for unknown parameters. You can form `solinit` with the helper function `bvpinit`. See the `bvpinit` reference page for details.

The output argument sol is a structure created by the solver. In the basic case the structure has fields x, y, and yp.

sol.x
Nodes of the mesh selected by bvp4c

sol.y
Approximation to at the mesh points of sol.x

sol.yp
Approximation to at the mesh points of sol.x

sol.parameters
Value of unknown parameters, if present, found by the solver.

sol.solver
'bvp4c'

`sol.x`	Nodes of the mesh selected by `bvp4c`
`sol.y`	Approximation to at the mesh points of `sol.x`
`sol.yp`	Approximation to at the mesh points of `sol.x`
`sol.parameters`	Value of unknown parameters, if present, found by the solver.
`sol.solver`	`'bvp4c'`

The function deval uses the output structure sol to evaluate the numerical solution at any point from [a,b].

Additional BVP Solver Arguments

For more advanced applications, you can also specify as input arguments solver options and additional known parameters.

options
Structure of optional parameters that change the default integration properties. This is the fourth input argument.
sol = bvp4c(odefun,bcfun,solinit,options)
Creating and Maintaining a BVP Options Structure tells you how to create the structure and describes the properties you can specify.

p1,p2...
Known parameters that the solver passes to odefun and bcfun.
sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...)
The solver passes any input parameters that follow the options argument to odefun and bcfun every time it calls them. Use options = [] as a placeholder if you set no options. In the odefun argument list, known parameters follow x, y, and a vector of unknown parameters (parameters), if present.
dydx = odefun(x,y,p1,p2,...) dydx = odefun(x,y,parameters,p1,p2,...)

In the bcfun argument list, known parameters follow ya, yb, and a vector of unknown parameters, if present.
res = bcfun(ya,yb,p1,p2,...) res = bcfun(ya,yb,parameters,p1,p2,...)
See Example: Using Continuation to Solve a Difficult BVP for an example.

`options`	Structure of optional parameters that change the default integration properties. This is the fourth input argument. sol = bvp4c(odefun,bcfun,solinit,options) Creating and Maintaining a BVP Options Structure tells you how to create the structure and describes the properties you can specify.
`p1,p2...`	Known parameters that the solver passes to `odefun` and `bcfun`. sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...) The solver passes any input parameters that follow the `options` argument to `odefun` and `bcfun` every time it calls them. Use `options` = `[]` as a placeholder if you set no options. In the `odefun` argument list, known parameters follow `x`, `y`, and a vector of unknown parameters (`parameters`), if present. dydx = odefun(x,y,p1,p2,...) dydx = odefun(x,y,parameters,p1,p2,...)
	In the `bcfun` argument list, known parameters follow `ya`, `yb`, and a vector of unknown parameters, if present. res = bcfun(ya,yb,p1,p2,...) res = bcfun(ya,yb,parameters,p1,p2,...) See Example: Using Continuation to Solve a Difficult BVP for an example.

Introduction to Boundary Value ODE Problems Solving BVP Problems