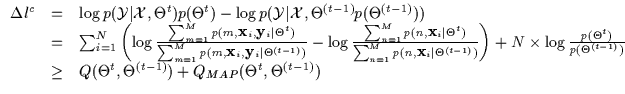Next: Implementation and Interpretation
Up: CEM for Gaussian Mixture
Previous: Bounding Matrices: The Gate
We have demonstrated a conditional maximum likelihood algorithm for a
conditioned mixture of Gaussians. Essentially, this optimized the
likelihood of the data given a model
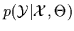 .
If a prior on the model
.
If a prior on the model 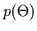 is given, we can perform MAP
estimation simply by computing a bound on the prior as well. Recall
that we had bounded the conditional log-likelihood (as in
Equation 7.6) using a Q function. We depict the
inclusion of a prior in Equation 7.32. Note how this does not
change the derivation of the maximum conditional likelihood solution
and merely adds one more bound for the prior to the N bounds
computed for each data point for the MLc solution. In fact, the
optimization of the prior is identical as it would be for a joint
density maximum a posteriori problem (MAP) and the fact that we are
optimizing MAPc does not affect it. Thus, a prior on a conditioned
mixture model being update with CEM will can be bounded exactly as a
prior on a normal mixture model being updated with EM. In theory, it
is thus possible to add to the above CEM derivation a variety of
priors including non-informative priors, conjugate priors, entropic
priors and so on.
is given, we can perform MAP
estimation simply by computing a bound on the prior as well. Recall
that we had bounded the conditional log-likelihood (as in
Equation 7.6) using a Q function. We depict the
inclusion of a prior in Equation 7.32. Note how this does not
change the derivation of the maximum conditional likelihood solution
and merely adds one more bound for the prior to the N bounds
computed for each data point for the MLc solution. In fact, the
optimization of the prior is identical as it would be for a joint
density maximum a posteriori problem (MAP) and the fact that we are
optimizing MAPc does not affect it. Thus, a prior on a conditioned
mixture model being update with CEM will can be bounded exactly as a
prior on a normal mixture model being updated with EM. In theory, it
is thus possible to add to the above CEM derivation a variety of
priors including non-informative priors, conjugate priors, entropic
priors and so on.
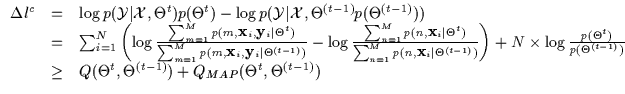 |
|
|
(7.32) |




Next: Implementation and Interpretation
Up: CEM for Gaussian Mixture
Previous: Bounding Matrices: The Gate
Tony Jebara
1999-09-15