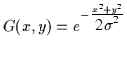 ,
the first derivative in
the x and y is:
,
the first derivative in
the x and y is:
In choosing our features, we were inspired by the object recognition
system proposed by Schiele and Crowley [12]. Objects are
represented as multidimensional histograms of vector responses of
local operators. Schiele experimentally compared the invariant
properties of a few receptive field functions, including Gabor filter
and local derivative operators. His results showed that Gaussian
derivatives provided the most robust and equivariant recognition
results. Given the Gaussian distribution
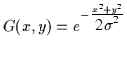 ,
the first derivative in
the x and y is:
,
the first derivative in
the x and y is:
![]() and
and
![]() .
The Laplace operator is
Lap(x,y) = Gxx(x,y) +
Gyy(x,y), where
.
The Laplace operator is
Lap(x,y) = Gxx(x,y) +
Gyy(x,y), where
![]() ,
,
![]() .
.
In our experiment, we used only the first derivative and the Laplacian at two different scales resulting in a 6 dimensional histogram. The resolution of the histogram axis was either 16 or 32 pixels. For more details on creating the histograms please refer to [12].
The probability of an object On given local measurement Mk is obtained using Bayes' rule:
where p(On) is the prior probability of the object which is known
and p(Mk) as the prior probability of the filter output which is
measured as
![]() .
So,
p(Mk|Oi), the
probability density of an object On differs from the
multi-dimensional histogram of an object by a normalization term. If
we have K independent measurements
M1, M2, ... ..., MK then the
probability of the object On is:
.
So,
p(Mk|Oi), the
probability density of an object On differs from the
multi-dimensional histogram of an object by a normalization term. If
we have K independent measurements
M1, M2, ... ..., MK then the
probability of the object On is:
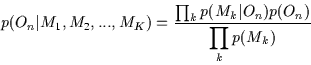
To ensure independence between measurements, we choose the minimum
distance
![]() between two measurements
Mk1 and Mk2. The measurement locations can be chosen
arbitrarily and it is not necessary have measurements at corresponding
points and only a certain number of local receptive field vectors need
to be calculated, the method is fast and robust to partial occlusion.
between two measurements
Mk1 and Mk2. The measurement locations can be chosen
arbitrarily and it is not necessary have measurements at corresponding
points and only a certain number of local receptive field vectors need
to be calculated, the method is fast and robust to partial occlusion.
Because we are trying to distinguish changes in the same object as
opposed to different objects we incorporate some motion cues into our
histograms by using difference images, which significantly improve the
performance. To capture both fast and slow changes, temporal
differencing should be done at different rates. However, for short
time scale or fast expressions it is enough to have consecutive frame
differencing of images recorded at 30 frames/second. In the original
framework of Schiele and Crowley [12] the histograms were
compared directly using the ![]() statistic, histogram intersection, or
mahalanobis distance. In our case, it is important to see changes in
the histograms over time for an expression rather than compare
histograms. Thus, to compactly represent the histograms and reduce the
dimensionality for temporal modeling we take the PCA of the input
histograms and use the top 20 eigenvectors, which capture 90% of the
variance to represent the histogram space.
statistic, histogram intersection, or
mahalanobis distance. In our case, it is important to see changes in
the histograms over time for an expression rather than compare
histograms. Thus, to compactly represent the histograms and reduce the
dimensionality for temporal modeling we take the PCA of the input
histograms and use the top 20 eigenvectors, which capture 90% of the
variance to represent the histogram space.