


Next: Mapping Residuals to Spatial
Up: Structure from Motion
Previous: Stable Representation for Recursive
As was discussed previously, each feature tracker recovers an optimal
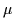 motion parameter by minimizing
motion parameter by minimizing
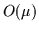 .
However,
since the 2D feature tracking in question was being used to recover
translation, rotation and scale, the
.
However,
since the 2D feature tracking in question was being used to recover
translation, rotation and scale, the 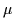 vector has 4 degrees
of freedom (not merely 2). We can represent these 4 degrees of freedom
as 2 point features that are free to translate independently. In other
words, two arbitrary points on the correlation window are selected
(i.e. 2 opposing corners) and it is trivial to compute their locations
from a corresponding
vector has 4 degrees
of freedom (not merely 2). We can represent these 4 degrees of freedom
as 2 point features that are free to translate independently. In other
words, two arbitrary points on the correlation window are selected
(i.e. 2 opposing corners) and it is trivial to compute their locations
from a corresponding 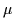 transformation (translation, scale
and rotation). This mapping goes both ways and we can model the 2D
tracking for each image patch with the SSD model using
transformation (translation, scale
and rotation). This mapping goes both ways and we can model the 2D
tracking for each image patch with the SSD model using 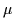 or
using the positions of 2 distinct feature points somewhere within the
window
(X1, Y1, X2, Y2). For M correlation-based windows, we
compute the (X,Y) location of N=2M points. These feature points are
then arranged into the
or
using the positions of 2 distinct feature points somewhere within the
window
(X1, Y1, X2, Y2). For M correlation-based windows, we
compute the (X,Y) location of N=2M points. These feature points are
then arranged into the 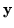 vector for input into the EKF.
vector for input into the EKF.
Tony Jebara
1999-12-07