We can represent these 2-D regions by their low-order statistics.
Clusters of 2-D points have 2-D spatial means and covariance matrices,
which we shall denote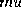 
and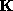 
. The blob spatial statistics
are described in terms of their second-order properties; for computational
convenience we will interpret this as a Gaussian model:
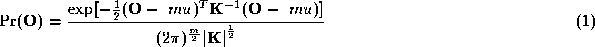
The Gaussian interpretation is not terribly significant, because we also
keep a pixel-by-pixel support map showing the actual occupancy. We
define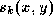 
, the support map for blob k, to be
The aggregate support map s(x,y) over all the blob models represents the
segmentation of the image into spatio-color classes.
Like other representations used in computer vision and signal analysis, including superquadrics, modal analysis, and eigenvector representations, blobs represent the global aspects of the shape and can be augmented with higher-order statistics to attain more detail if the data supports it. The reduction of degrees of freedom from individual pixels to blob parameters is a form of regularization which allows the ill-conditioned problem to be solved in a principled and stable way.
Each blob has a spatial (x,y) and color (Y,U,V) component. Color is
expressed in the YUV color space. We could additionally use motion and
texture measurements as part of the blob descriptions, but current hardware
has restricted us to use position and color only. Because of their
different semantics, the spatial and color distributions are assumed to be
independent. That is,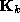 
is block-diagonal, with uncoupled
spatial and spectral components. Each blob can also have a detailed
representation of its shape and appearance, modeled as differences from the
underlying blob statistics. The ability to efficiently compute compact
representations of people's appearance is useful for low-bandwidth
applications[5].
The statistics of each blob are recursively updated to combine information contained in the most recent image with knowledge contained in the current class statistics and the priors.