Mathematics

QR Factorization

An orthogonal matrix, or a matrix with orthonormal columns, is a real matrix whose columns all have unit length and are perpendicular to each other. If Q is orthogonal, then

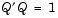
The simplest orthogonal matrices are two-dimensional coordinate rotations.

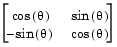
For complex matrices, the corresponding term is unitary. Orthogonal and unitary matrices are desirable for numerical computation because they preserve length, preserve angles, and do not magnify errors.

The orthogonal, or QR, factorization expresses any rectangular matrix as the product of an orthogonal or unitary matrix and an upper triangular matrix. A column permutation may also be involved.

or

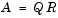
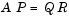
where Q is orthogonal or unitary, R is upper triangular, and P is a permutation.

There are four variants of the QR factorization- full or economy size, and with or without column permutation.

Overdetermined linear systems involve a rectangular matrix with more rows than columns, that is m-by-n with m > n. The full size QR factorization produces a square, m-by-m orthogonal Q and a rectangular m-by-n upper triangular R.

• [Q,R] = qr(C)
  
  Q =
     -0.8182    0.3999   -0.4131
     -0.1818   -0.8616   -0.4739
     -0.5455   -0.3126    0.7777
  
  R =
    -11.0000   -8.5455
           0   -7.4817
           0         0
  

In many cases, the last m - n columns of Q are not needed because they are multiplied by the zeros in the bottom portion of R. So the economy size QR factorization produces a rectangular, m-by-n Q with orthonormal columns and a square n-by-n upper triangular R. For our 3-by-2 example, this is not much of a saving, but for larger, highly rectangular matrices, the savings in both time and memory can be quite important.

• [Q,R] = qr(C,0)
  
  Q =
     -0.8182    0.3999
     -0.1818   -0.8616
     -0.5455   -0.3126
  
  R =
    -11.0000   -8.5455
           0   -7.4817
  

In contrast to the LU factorization, the QR factorization does not require any pivoting or permutations. But an optional column permutation, triggered by the presence of a third output argument, is useful for detecting singularity or rank deficiency. At each step of the factorization, the column of the remaining unfactored matrix with largest norm is used as the basis for that step. This ensures that the diagonal elements of R occur in decreasing order and that any linear dependence among the columns is almost certainly be revealed by examining these elements. For our small example, the second column of C has a larger norm than the first, so the two columns are exchanged.

• [Q,R,P] = qr(C)
  
  Q =
     -0.3522    0.8398   -0.4131
     -0.7044   -0.5285   -0.4739
     -0.6163    0.1241    0.7777
  
  R =
    -11.3578   -8.2762
           0    7.2460
           0         0
  
  P =
       0     1
       1     0
  

When the economy size and column permutations are combined, the third output argument is a permutation vector, rather than a permutation matrix.

• [Q,R,p] = qr(C,0)
  
  Q =
     -0.3522    0.8398
     -0.7044   -0.5285
     -0.6163    0.1241
  
  R =
    -11.3578   -8.2762
           0    7.2460
  
  
  p =
       2     1
  

The QR factorization transforms an overdetermined linear system into an equivalent triangular system. The expression

• norm(A*x - b)
  

is equal to

• norm(Q*R*x - b)
  

Multiplication by orthogonal matrices preserves the Euclidean norm, so this expression is also equal to

• norm(R*x - y)
  

where y = Q'*b. Since the last m-n rows of R are zero, this expression breaks into two pieces

• norm(R(1:n,1:n)*x - y(1:n))
  

and

• norm(y(n+1:m))
  

When A has full rank, it is possible to solve for x so that the first of these expressions is zero. Then the second expression gives the norm of the residual. When A does not have full rank, the triangular structure of R makes it possible to find a basic solution to the least squares problem.

LU Factorization

Matrix Powers and Exponentials