Data Analysis and Statistics (Mathematics)

Mathematics

Difference Equations and Filtering

MATLAB has functions for working with difference equations and filters. These functions operate primarily on vectors.

Vectors are used to hold sampled-data signals, or sequences, for signal processing and data analysis. For multi-input systems, each row of a matrix corresponds to a sample point with each input appearing as columns of the matrix.

The function

```
y = filter(b,a,x)
```

processes the data in vector x with the filter described by vectors a and b, creating filtered data y.

The filter command can be thought of as an efficient implementation of the difference equation. The filter structure is the general tapped delay-line filter described by the difference equation below, where n is the index of the current sample, na is the order of the polynomial described by vector a and nb is the order of the polynomial described by vector b. The output y(n), is a linear combination of current and previous inputs, x(n) x(n-1) ..., and previous outputs, y(n-1) y(n-2) ...

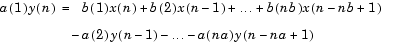
Suppose, for example, we want to smooth our traffic count data with a moving average filter to see the average traffic flow over a 4-hour window. This process is represented by the difference equation

The corresponding vectors are

```
a = 1;
b = [1/4 1/4 1/4 1/4];
```

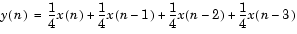
Note Enter the format command, format rat, to display and enter data using the rational format.

Executing the command

```
load count.dat
```

creates the matrix count in the workspace.

For this example, extract the first column of traffic counts and assign it to the vector x.

```
x = count(:,1);
```

The 4-hour moving-average of the data is efficiently calculated with

```
y = filter(b,a,x);
```

Compare the original data and the smoothed data with an overlaid plot of the two curves.

t = 1:length(x);
plot(t,x,'-.',t,y,'-'), grid on
legend('Original Data','Smoothed Data',2)

The filtered data represented by the solid line is the 4-hour moving average of the observed traffic count data represented by the dashed line.

For practical filtering applications, the Signal Processing Toolbox includes numerous functions for designing and analyzing filters.

The Basic Fitting Interface Fourier Analysis and the Fast Fourier Transform (FFT)